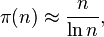tricky way to find out Ugly Number(at LeetCode)

For the given question in LeetCode.com, https://leetcode.com/problems/ugly-number/

I coded kind of tricky logic to solve this question.

Ugly number is number which is only divided by three prime numbers; 2, 3, 5 (1 is considered as Ugly Number)

At first, I tried this and got time limit error.

    bool isUgly(int num) {
        if(num == 1) return true;
        do{
            if(num % 2 == 0) { num /= 2; continue; }
            if(num % 3 == 0) { num /= 3; continue; }
            if(num % 5 == 0) { num /= 5; continue; }
            if(num == 1) return true;
            return false;
        } while(1);
    }

Well, if very big number is given, there might be lots of loop.


So I added one line below and I got Accepted with 8 msec runtime.

if(num % 7 == 0) { return false; }

Fine, but unsatisfied because someone got faster result.

So I added more conditions and final code is this:

    bool isUgly(int num) {
        if(num == 1) return true;
        do{
            if(num % 7 == 0) { return false; }
            else if(num % 11 == 0) { return false; }
            else if(num % 13 == 0) { return false; }
            else if(num % 17 == 0) { return false; }
            else if(num % 19 == 0) { return false; }
            else if(num % 23 == 0) { return false; }

            if(num % 2 == 0) { num /= 2; continue; }
            if(num % 3 == 0) { num /= 3; continue; }
            if(num % 5 == 0) { num /= 5; continue; }
            
            if(num == 1) return true;
            return false;
        } while(1);
        
        
    }

Finally I got Accepted with 4 msec runtime.

Heh, lucky.

This code might be silly like a undergraduate student's job but shows good performance for the LeetCode examples.

I don't know how big numbers should be evaluated for the Ugly Number but most numbers might have small prime factors like 2, 3, 5, 7, 11, 13 blar blar..

I am not a mathematician and I cannot speculate the way of getting prime factors effectively.

However, If you just divide the given number with few prime numbers such as 7, 11, 13 ... 23, you can quickly make it.

According to Wikipedia, the number of prime numbers below a given number is approximately like this: